Un blog Low-Tech

15 novembre 2020

Interlude: ensemble de Mandelbrot en Maple V

A l'occasion du rangement d'une armoire, mes parents ont retrouvé le CD d'installation de Maple V ("Version 4 pour Windows et Macintosh") que j'avais utilisé en 1997-1998 pour mes études. Le CD étant intact, ainsi que les livres qui l'accompagnent, j'ai tenté une installation dans un environnement "vintage" compatible avec ce logiciel.

Pour cela j'ai utilisé une machine virtuelle en Windows NT 3.51 SP5 dénichée sur le site win3x.org. Après avoir mappé le lecteur CD de mon PC sur celui de la machine virtuelle, j'ai pu lancer l'installation de Maple.

Voici un aperçu de l'environnement obtenu :

A l'époque où j'utilisais ce logiciel, j'avais développé un algorithme bien laborieux qui traçait un ensemble de Mandelbrot. J'ai donc retenté le coup, en produisant le code suivant :

M := (x,c) -> x^2 + c;

MandelbrotMax :=
    proc(nMax, max, x, y)
    local c, i, temp, tempabs;
    c := x + y*I;
    temp := 0;
    tempabs := abs(temp);
    i := 0;
    if (tempabs <= max)
        then
            while tempabs <= max and i < nMax
                do
                    temp := M(temp,c);
                    tempabs := abs(temp);
                    i := i+1;
                od;
    fi;
    if i = nMax then 1 else 0; fi;
end;

MandelPlot := (x,y) -> MandelbrotMax(1000,2,x,y);

plot3d(MandelPlot, -2..1, -1..1, numpoints=10000, orientation = [-90,0], axes=normal, style=patchnogrid, scaling=constrained);
}

Et ça marche! Il faut juste 50 secondes de calcul pour produire le graphique suivant (au lieu d'une bonne heure voire beaucoup plus, à l'époque)

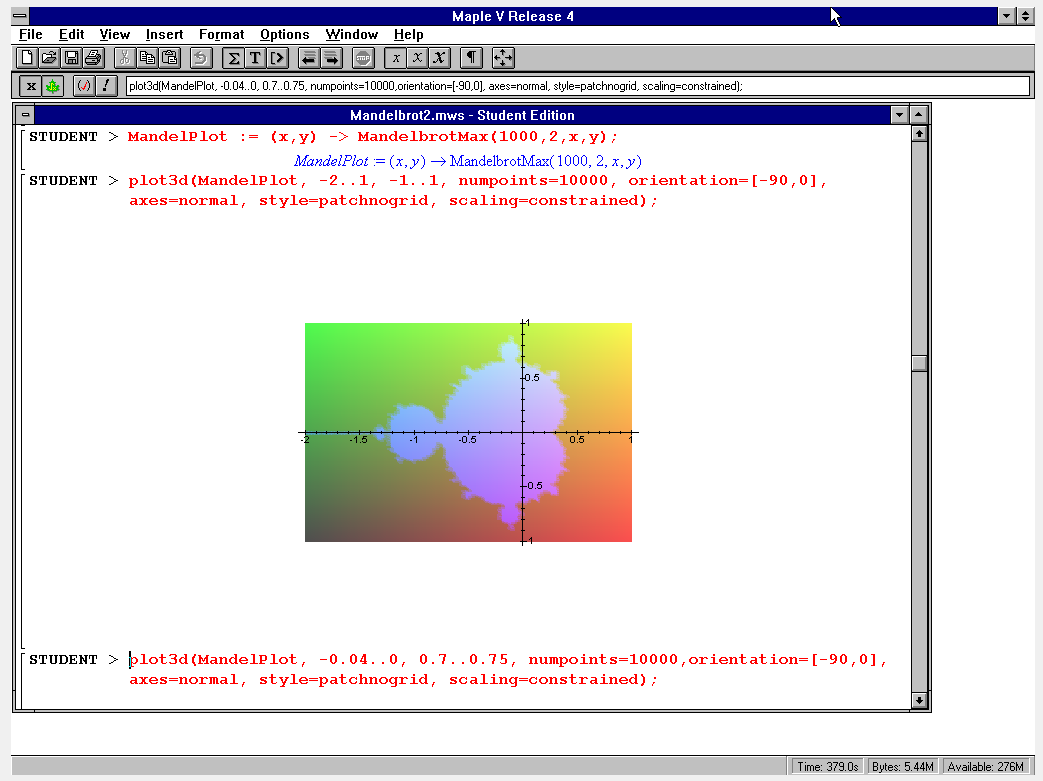
J'espère que ce petit interlude vous aura plu. En tout cas je me suis bien amusé.

---